2015年3月5日 星期四

資料保密的方法

資料保密的方法
(線上交易安全系列2/4)

By 陳宜誠 Vincent Chen

（這是我於西元1995~1997年發表於『網際空間』雜誌之“CyberMoney” 和 “CyberTech” 專欄，並以《網際理財。海外投資：兼論網路交易安全》，ISBN 957-99499-6-4，由資訊傳真機構於西元1997年9月集結成書出版的幾篇文章。現在回頭再看它們，覺得雖然經過了快二十年了，這些有關線上交易安全的資訊對於網友可能還算有用，所以再PO這些文章在這裡，以跟網友共勉之。）





資料保密的方法



保密（Cryptography）技術是一種編碼的方法，用來確保１）只有受信人才能夠了解信件的內容，２）能證實發信方的真實身分，３）而且還能夠驗證信件的內容並沒有被竄改。 資訊加密的程序（Encryption Algorithm）有很多，可以概分為「祕密金匙」（Secret Key）和「公開金匙」（Public Key）兩大類。


祕密的單一金匙（Single Key）系統



移形換位的單一金匙加密法



據說古代羅馬帝國的凱撒大帝在出外攻打他國時，為了怕送信的郵差、對抗的敵人，或在羅馬的政敵們，會去偷閱他跟元老院同僚的郵件和軍令（或者是他跟埃及艷后間的情書），就發明了一套很簡單的文件加密法則。 他是把文件中的各個字元用羅馬字元表裡（咦？ 羅馬人是用羅馬字母吧？）向後數的第三個字元來取代。 以二十六個英文字母來說（先不管標點符號，大小寫，空白，及換行等等），就是把“This is a book“這句話，寫成“Wklv lv d erre“。 解這個密件時，反過來做就行了。 這裡所用的密碼，就是一個[+3]的數字。 有些Newsgroup信件上所用的ROT-13（Rotate 13）加密法，也是屬於此類方法。 加密時把原文的英文字母用字母表上向後數１３位的字母來取代的，解密時用向前數１３位的字母來取代回來即可。


把這個換位（Transportation）的加密原則推廣到一組為八個位元，我們就可使用八個數字為一組密碼。 例如，假若密碼是[+5][-11][-1][+8][+7][-5][+3][+2]，就是第一個字元換成由它向後數的第五個字母，第二個字元換成向前數第十一個字母，以此類推。 到了第九個位元時，再重頭循環使用第一個密碼數字。 如此這樣，只要凱撒用不同的密碼組合寫信給各個收信人，就可以跟不同的人以祕密的方式通信。 而任何人只要知道自己的密碼為何，就能夠解開凱撒送來的密件，而且不用擔心會有人造假或能夠偷看內容。


到了電子時代，這個換位的方法仍可以適用，只是對象縮小為輸入資料的每一個位元（bit），而換位的範圍擴大為八個位元組（bytes），而且又可加入另外的一個移形（toggle）觀念，也就是把１變成０，０變成１。 所以，您就照著金匙（Key）裡面的每一個位元，來決定輸入的明碼（Clear Text），要不要被系統化的移型（Transport）或換位(Toggle)，成為密碼（Cipher Text）。 而這個系統化的方法，就是加密/解密使用的程序（Encrypt/Decrypt Procedure）。 而程序必須是相同的，金匙才能夠共用，雙方才能夠建立通信的管道。

這個共通的金匙，不但用來加密／解密，而且可以用來證明信件的真偽，所以是個通信雙方必須保持的祕密（Secret）。 所以，這些金匙必須儲存在一個安全的地方，例如只存在人的腦袋裡，或放在硬體設施裡用保全裝置（Tamper Resist）來保護（所謂硬體加密），不能存在檔案系統裡用軟體的方法來保護（所謂軟體加密）。 而加密／解密的程序到底是用特殊晶片（IC Chip），韌體（Firmware），或軟體（Software）程式來執行，倒是無所謂，只牽涉到執行的速度，跟保全的要求無關。 而同一個金匙，用久了就會增加被破解的可能性，所以要時常更換。 所以這個祕密金匙必須雙方預先設定，或由已知的安全通信管道來傳遞或更換，也是敵方亟欲擷取的標的物。 在這邊，讀者可以看到一個雞生蛋、蛋生雞的矛盾。 假如我們已經有一個安全的通信管道可以用來傳遞金匙，那為什麼我們不直接用它來傳遞文件就好了，可見並沒有所謂安全的通信管道，而廣為大家所採用的方法，就是把一個金匙分為好幾個部份（Key Parts），各個部分都經過不同的人及不同的一般通信管道（例如電話，Fax，郵件，Email，檔案等）在不同的時間來傳遞，以藉此製造出一個相對安全的通信管道。 這類祕密金匙的管理和傳遞（Key Management and Key Distribution）一直是個重大的課題，而ANSI X.19就是規定一個有關金匙的管理和傳遞方面所必須遵循的共通標準。

恭喜您，看到這裡您還能夠看得懂得話，你已經了解了基本的加密／解密法則了。 以下是幾種較常見的祕密金匙加密程序。

DES


最廣為採用的祕密金匙加密程序就是DES。DES就是「資料加密標準」“The Data Encryption Standard”的字首英文縮寫。 在1974，美國National Bureau of Standards (NBS)，就是現在美國NIST (National Institute of Standards and Technology)的前身，感到有制定官方通用加密程序的需求，於是公開徵求有關「標準資料加密程序」的各方提案。 最後它終於收到由IBM以其先前發展的LUCIFER加密程序為基準所發展的一套DES加密程序。 在一系列的嚴密測試和不知為何的（據稱是考量當時電腦的運算速度）將金匙長度由112位元減少為56位元後，DES於November 23, 1976正式成為美國官方的加密標準，而且被授權用來保護所有非機密（unclassified）的官方通訊。

於是，DES於1977年開始，每五年由NIST正式認證為美國政府機構所有「次於最高機密的機密文件」（less-than-top-secret secret material）的官方加密標準。 這個官方加密標準，照規定每五年必須重新由NIST認證一次，以確定能抵禦敵方破解的最新招數。 DES最近通過的一次認證是在1993年，但由於近年來破解密碼的數學技巧和電腦運算速度的大幅進步，DES很可能會過不了下一次NIST於1998年的認證。 但直到現在仍未有其他可以取代DES的官方加密標準被NIST認證過，或甚至有被任何人提出來。 我們可以合理的推測，下一個會被NIST認證的官方加密標準，將仍是DES或其變型，只是其金匙長度應會適度增長。

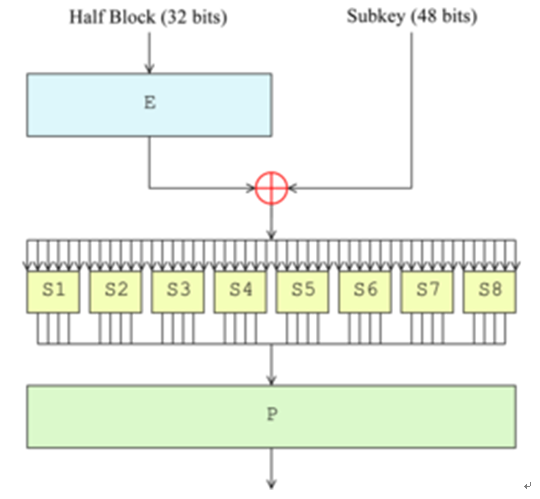
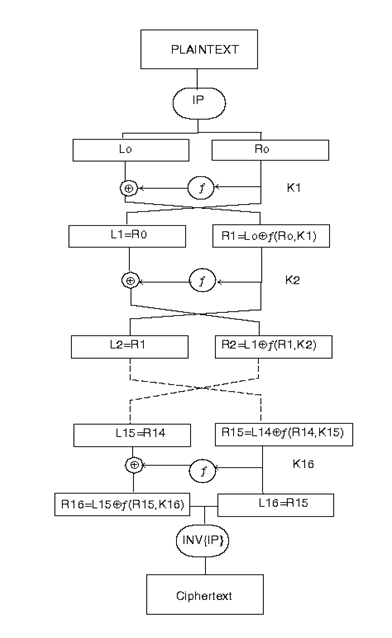
DES是區段加密（block cipher）的程序，意思是說原文（plaintext）是以固定區段長度（block size）的資料來做加密，而非應用到單個位元的串列加密（stream cipher）程序。DES的區段長度是64位元，而它的金匙長度是56位元（DES金匙是以８個位元組（Byte），就是64位元來表示，每個位元組的第８個位元是偵錯（parity check）的位元，與加密運算無關）。DES只用到加密演算法的最基本的兩種運算：diffusion和confusion。 輸入的資料將會被運算16次，每一次叫做一回合（round）。 在每回合中是否使用及如何使用diffusion和confusion這兩種運算則由金匙來決定。 如下圖所示。




　

The Feistel function (F function) of DES

Designer(s):
IBM

First published:
1975 (standardized on January 1977)

Derived from:
Lucifer

Successor(s):
Triple DES, G-DES, DES-X, LOKI89, ICE

Key size(s):
56 bits

Block size(s):
64 bits

Structure:
Feistel network

Rounds:
16

Best public cryptanalysis:

DES is now considered insecure because a brute force attack is possible (see EFF DES cracker). As of 2004, the best analytical attack is linear cryptanalysis, which requires 243 known plaintexts and has a time complexity of 239-43 (Junod, 2001); under a chosen-plaintext assumption, the data complexity can be reduced by a factor of four (Knudsen and Mathiassen, 2000).




3-DES

有人開始用 Triple-DES 等來加長金匙的長度，就是把兩個Ａ與Ｂ的 DES 金匙合起來用，對於資料以【Ａ加密，Ｂ解密，Ａ加密】的加密，和【Ａ解密，Ｂ加密，Ａ解密】的解密方式，把金匙的長度增長為兩倍，成為 102 位元，讓保密的程度一下子推進了上萬倍。

AES




　

The SubBytes step, one of four stages in a round of AES

Designer(s):
Vincent Rijmen, Joan Daemen

First published:
1998

Derived from:
Square

Successor(s):
Anubis, Grand Cru

Certification:
AES winner, CRYPTREC, NESSIE

Key size(s):
128, 192 or 256 bits[1]

Block size(s):
128 bits[2]

Structure:
Substitution-permutation network

Rounds:
10, 12 or 14 (depending on key size)

Best public cryptanalysis:

A related-key attack can break up to 9 rounds of 256-bit AES. A chosen-plaintext attack can break 8 rounds of 192- and 256-bit AES, and 7 rounds of 128-bit AES. (Ferguson et al, 2000).

Advanced Encryption Standard (AES), 又稱Rijndael, 是一種區段式加密法則(block cipher) 已經於2002年五月被National Institute of Standards and Technology (NIST) 選為美國政府的官方加密法則,並訂為U.S. FIPS PUB 197 (FIPS 197)取代DES成為新的國家加密標準. AES與DES已成為最常用的對稱性加密法則(symmetric key cryptography).

此加密法則由兩位比利時密碼學專家, Joan Daemen 及 Vincent Rijmen, 發展出來的,兩人皆任教於Katholieke Universiteit Leuven大學, 在遴選AES的運算法則時,從眾多入圍候選名單裡,被NIST評審委員會選為AES所用的加密法則.

RC4


RC4是RSA Data Security, Inc.所發展的一套祕密金匙加密程序。 直到有人把它的原始程式碼（source code）放到網路論壇（Usenet Newsgroup）之前，RC4本來是個商業機密（trade secret）。 RC4的主要好處是它的速度超快。 只要用Intel的486電腦來運算，RC4每秒鐘就可處理數百Ｋ位元組的資料。 我們尚不能確知RC4是否像DES一樣被證明為是「強悍的加密程序」（strong cipher），但至少到現在為止還沒有輕易破解它的報導。RSA還有RC2和RC5等相關的加密程序。

讀者會感到有興趣的是，可以外銷的SSL (Netscape所用的Secure Socket Layer)版本，使用的是金匙長度為40個位元的RC4-40，它於1997年初已分別被至少兩組不同的人馬，前後共花了８天的時間所破解。 所以，我們可以確知RC4-40並不能保障您的資料通信安全。

RC4 generates a pseudorandom stream of bits (a "keystream") which, for encryption, is combined with the plaintext using XOR as with any Vernam cipher; decryption is performed the same way. To generate the keystream, the cipher makes use of a secret internal state which consists of two parts:

1.     A permutation of all 256 possible bytes (denoted "S" below).

2.     Two 8-bit index-pointers (denoted "i" and "j").

The permutation is initialised with a variable length key, typically between 40 and 256 bits, using the key-scheduling algorithm (KSA). Once this has been completed, the stream of bits is generated using the pseudo-random generation algorithm (PRGA).

The key-scheduling algorithm (KSA)

The key-scheduling algorithm is used to initialise the permutation in the array "S". "keylength" is defined as the number of bytes in the key and can be in the range 1 ≤ keylength ≤ 256, typically between 5 and 16, corresponding to a key length of 40 – 128 bits. First, the array "S" is initialised to the identity permutation. S is then processed for 256 iterations in a similar way to the main PRGA algorithm, but also mixes in bytes of the key at the same time.

for i from 0 to 255


    S[i] := i


j := 0


for i from 0 to 255


    j := (j + S[i] + key[i mod keylength]) mod 256


    swap(S[i],S[j])


The pseudo-random generation algorithm (PRGA)


The lookup stage of RC4. The output byte is selected by looking up the values of S(i) and S(j), adding them together modulo 256, and then looking up the sum in S; S(S(i) + S(j)) is used as a byte of the key stream, K.

For as many iterations as are needed, the PRGA modifies the state and outputs a byte of the keystream. In each iteration, the PRGA increments i, adds the value of S pointed to by i to j, exchanges the values of S[i] and S[j], and then outputs the value of S at the location S[i] + S[j] (modulo 256). Each value of S is swapped at least once every 256 iterations.

i := 0


j := 0


while GeneratingOutput:


    i := (i + 1) mod 256


    j := (j + S[i]) mod 256


    swap(S[i],S[j])


    output S[(S[i] + S[j]) mod 256]


IDEA


IDEA (International Data Encryption Algorithm)是瑞士ETH Zurich所發展的祕密金匙加密程序。IDEA被視為現今最好而且是最安全的加密演算法。 它使用128位元的金匙來加密一個64位元的資料區間，而且它是對稱的（Symmetric），同一個加密程序可以用來作加密（encryption）和解密（decryption）。 它只發表了幾年而已，還是很新的演算法，所以還沒有足夠的人試圖去破解它，以證明它是足夠強悍。

Skipjack


Skipjack是美國「國家安全局」NSA（National Security Agency）為Clipper和 Capstone加密晶片所發展的祕密金匙加密程序。它的演算法被列為機密。 我們已知的是，它是個對稱的加密程序，使用80位元的金匙，而且輸入資料將會被它運算32個回合。

公開的成對金匙（Private/Public Key Pair）系統


兩兩成對的公開金匙加密法


近來保密系統的發展，除了增加解密的難度外（就是增加金匙的長度），就是使用成對的（Key Pair）、非對稱性（Asymmetric）的公開金匙加密程序。

公開金匙加密程序，使用的是一道數學難題的答案和題目之間，成對的一組解。 這情況就像，某人可以告訴大家他旅館房間的號碼（Public Key），但別人只能把東西透過櫃台送進去（Encrypt/Cipher），只有他可以用房間鑰匙（Private Key）開門，進入房間去取得物品（Decrypt/Decipher）。 所以，你可以用他人的公開密碼來加密一個訊息，然後再送給對方，不用擔心會被人截收或竄改，收到密文後，對方就可以用他的私人密碼來解開這個訊息了。

這邊有幾個有趣的現象出現。 第一個是數位簽章（Digital Signature）的應用。 同上所述的方法，送信方可以用自己的私人密碼（Private Key）來加密一個訊息，以產生一個數位簽名（訊息摘要／姓名／服務機構／職稱等資料），連同訊息傳送給收信方。 產生訊息摘要的方法很多，都是使用所謂的篩選函數（Hash Function）來作。 收信方可以用送信方的公開密碼（Public Key）來解密這個數位簽名，並用同樣的篩選函數來重算這個信息的訊息摘要，以供比對之用。 相符之後，便可證實此信息確實為送信方所送。 日後送信方若要抵賴，更可由公正第三人來依此仲裁，達到簽名在法律文件上的不可抵賴性。 這方面已有X.509國際標準出現。

第二個是如何取得他人正確的公開密碼，由誰來作這個發行、管理及認證數位簽章的艱鉅工作，還有跨國的交易清算及認證問題到底要如何解決。 以往有人採取在朋友之間互相傳播公開密碼的方法，結果效果不彰，且無公信力。 所以，成立一個能擔任公正第三人的認證中心（Certificate Authority）以及跨國建立一個認證體系（CA Hierarchy）就成為各國金融機構，清算中心，電信公司，信用組織，郵政單位，以及各級政府競相投入的工作了。 各國CA現今所使用的軟硬體研發器材以BBN Corp.的SafeKeyper為首，其在台總代理為台灣電腦（mailto:tsoung@ms8.hinet.net）。

第三個是如何保護數位簽章和所使用的篩選函數及文章摘要不被竄改等問題，還是要靠祕密金匙加密程序來解決。 由於公開加密法則是解開一個數學難題，運算繁雜所以速度較慢，只適合用來保護少量的資料。 實用上，訊息本身的保全還是用祕密金匙加密程序來進行，而公開金匙加密程序則是用來傳遞並保護所使用的祕密金匙。 所以，祕密金匙加密程序和公開金匙加密程序兩者不是對立的演算法則，而是相輔相成的加密程序。 以下是幾種常見的公開金匙加密程序。

RSA


最廣為人所熟知的公開金匙加密程序是MIT的”RSA encryption standard” (這個名字乃紀念其三個發明人Rivest，Shamir，和Adleman)。 其演算法如下。

RSA involves a public and private key. The public key can be known to everyone and is used for encrypting messages. Messages encrypted with the public key can only be decrypted using the private key. The keys for the RSA algorithm are generated the following way:
1.     Choose two large random prime numbers p \,and q \,
2.     Compute n = p q \,
o    n\,is used as the modulus for both the public and private keys
3.     Compute the totient: \phi(n) = (p-1)(q-1) \,.
4.     Choose an integer e\,such that 1 < e\,< \phi(n)\,, and e\,is coprime to \phi(n)\,ie: e\,and \phi (n)\,share no factors other than 1; gcd(e\,,\phi(n)\,) = 1.
o    e\,is released as the the public key exponent
5.     Compute d\,to satisfy the congruence relation d e \equiv 1\pmod{\phi(n)}\,ie: de = 1 + k\phi(n)\,for some integer k\,.
o    d\,is kept as the private key exponent  
－－－






DSA


這是一個產生數位簽章的方法，是ElGamal和Schnorr所提出的指數加密法（exponentiation cipher）的改良形式。 在1991年被DSA列為NIST Digital Signature Standard (DSS)的基準。

Key generation

  • Choose a 160-bit prime q.
  • Choose an L-bit prime p, such that p=qz+1 for some integer z, 512 ≤ L ≤ 1024, and L is divisible by 64.
    Note: FIPS-186-2, change notice 1 specifies that L should only assume the value 1024.
  • Choose h, where 1 < h < p − 1 such that g = hz mod p > 1. (Recall that z = (p-1) / q.)
  • Choose x by some random method, where 0 < x < q.
  • Calculate y = gx mod p.
  • Public key is (p, q, g, y). Private key is x.

Note that (p, q, g) can be shared between different users of the system, if desired.

The forthcoming FIPS 186-3 (described, e.g., in SP 800-57) uses SHA-224/256/384/512 as the hash function, q of size 224, 256, 384, and 512 bits, and L equal to 2048, 3072, 7680, and 15360, respectively.

There exist efficient algorithms for computing the modular exponentiations hz mod p and gx mod p. Most numbers h satisfy the requirement, so the value 2 is commonly used.

Signing


  • Generate a random per message value k where 0 < k < q
  • Calculate r = (gk mod p) mod q
  • Calculate s = (k-1(SHA-1(m) + x*r)) mod q, where SHA-1(m) is the SHA-1 hash function applied to the message m
  • Recalculate the signature in the unlikely case that r=0 or s=0
  • The signature is (r,s)

The extended Euclidean algorithm can be used to compute the modular inverse k-1 mod q.

Verifying


  • Reject the signature if either 0< r <q or 0< s <q is not satisfied.
  • Calculate w = (s)-1 mod q
  • Calculate u1 = (SHA-1(m)*w) mod q
  • Calculate u2 = (r*w) mod q
  • Calculate v = ((gu1*yu2) mod p) mod q
  • The signature is valid if v = r

DSA is similar to the ElGamal signature scheme.




篩選函數（Hash Function）和訊息摘要（Message Digest）


篩選函數（hash function） H 能接受一個變動長度的訊息 M 作為輸入，並輸出一個固定長度的訊息摘要（message digest） H(M) 。 通常 H(M) 會遠比 M 小；例如， H(M) 可能會是64或128位元，而 M 可以是一百萬位元組或更多。

篩選函數可以用來偵測訊息是否被竄改，也就是說，它可以用來產生 cryptographic checksum (又稱為 MDC = manipulation detection code 或 MAC = message authentication code)。 理論上，兩個不同的訊息有可能會產生同樣的訊息摘要，這樣的情形又稱為碰撞（collision）。 而安全的篩選函數要能盡量避免這樣的情況發生（collision avoidance）。


金匙的長度


根據密碼學專家的研究顯示，一般來說加密用的金匙長度每增加三位元，其破解的難度就增加一倍，也就是說敵方在不知道正確密碼而硬要破解這密碼所需花費的時間就至少要加上一倍。 所以，上面的密件假如改用56位元的金匙來加密，破解它所需花的時間，就會延長到至少好幾個月。 而用128位元的金匙來加密的話，用現在最快的超級電腦和已知最強的破解程序，至少還要花個千萬年才行。

當然，電腦的運算速度和破解密碼的方法也不是一成不變的，他們這十幾年來進步的幅度也遠超過密碼專家原先的預估，讓原先大家預期可以放心使用到下一個世紀的56位元DES，幾年前就有資料保全專家覺得不能用來保護絕對機密的資料了，於是有人開始用Triple-DES等來加長金匙的長度，就是把兩個Ａ與Ｂ的DES金匙合起來用，對於資料以【Ａ加密，Ｂ解密，Ａ加密】的加密，和【Ａ解密，Ｂ加密，Ａ解密】的解密方式，把金匙的長度增長為兩倍，成為102位元，讓保密的程度一下子推進了上萬倍。 所以幾個安全顧慮高的機構，對於內部的資料，現在要不是改用Triple-DES，就是改用RC4（可用長達128位元的金匙）等具有更長的金匙的加密標準了。 不過，為了能互相通信，對外的通信，他們還是繼續用DES，只是把更換金匙的頻率加快，讓重複使用同一金匙的機率大幅減少，以減少被入侵的可能性，和降低被人竊取或破壞的程度。

如上所述，DES加密程序所用的金匙長度為56位元，而Netscape SSL和RSA Public Key所採用的RC4加密程序也是類似DES的單金匙加密程序，但RC4可以使用非常長的金匙，例如128位元。 而以往美國的出口管制，限制美國的公司只能出口40個位元以下金匙長度的保密系統，所以您在Netscape國際版裡看到的SSL v2或v3都是使用40個位元的金匙而已。 如前所述，用40個位元的金匙所加密的文件，可以說只是稍具防護力，有心人只要有一台Pentium個人電腦和適當的程式，就能在兩三天內解開此密件。 詳情請參考相關站台 ”I broke Hal's SSL challenge” http://pauillac.inria.fr/~doligez/ssl/。 近來美國政府雖已將這項出口管制放寬為56位元，但跟大家希望的至少80位元的金匙長度，仍有很大的差距。

美國政府還規定，美國公司所生產或出口的任何保密系統都必須設計一把特殊的基準金匙作為後門（Back Door），並存放在公正機構（例如法院），以能在必要時輕易解開任何用這個保密系統所加密的機密文件。 簡單來說，它限制了其所產生的金匙，都必須落在以這個特殊金匙為基準的40位元的變化範圍內。 所以，Lotus Notes等美國公司製造的國際版產品，他們所用的保密程序若要能得到美國的出口許可，它表面上雖然用的是56個位元的DES或128個位元的RC4加密程序，但事實上其程式所產生的金匙都必須落在一個用40個位元就能涵蓋的變化範圍內，而其做為基準（base）的金匙就放在美國政府所指定的地方。 在法院授權的情況下，有了這個基準金匙，美國政府就可以像解開用40個位元的金匙所加密的文件那樣，輕易的去解開任何它想解開的密件。

原先美國政府強制任何加密系統都要留這個後門（Back Door）的表面原因是，避免外國間諜、黑社會、以及恐怖分子所傳遞的加密訊息，美國執法機關在截聽、側錄、或拷貝取得之後仍然無法破解或讀取，會危害美國廣義的國家安全（National Security）。 不過，這個立論本身就有不讓民間使用保密通信的味道，也有危害美國人最重視的隱私權的嫌疑，它最近已被某聯邦法官判定為違憲的行政法令，會危害美國憲法所保障的言論自由。 當然，美國政府對這項判決還在上訴中。 但是，究竟會有哪個外國公司或政府機構會這麼傻，在採購美國公司所生產的保密產品加以廣泛使用之後，還能容忍在美國某處，竟然會有這種能夠輕易破解並閱讀其機密文件的法寶呢？ 這是不可能的嘛。 試想，假如某金庫的美國製造商存有它製造的所有金庫的備份鑰匙，只要美國政府中某機關的某人覺得有需要，出個證明就能拿它來開啟你的金庫，你會放心購買這家產商的金庫嗎？ 所以，我認為美國政府的這個密碼長度和加上後門的出口限制，只會降低美國保密相關產品的國際競爭力，終究會被取消掉。

（

後註：前美國NSA探員史諾登最近說，NSA仍透過駭客手法，或上述的後門基準金匙，已取得SIM卡大廠的Master Key，使其能侵入幾乎任何人的手機，探取所傳輸或儲存的資訊，．．．
---

Gemalto 承認遭英美情報單位駭，眾人質疑六天時間那可能查出端倪
TechNews 科技新報



Gemalto 承認遭英美情報單位駭，眾人質疑六天時間那可能查出端倪
http://technews.tw/2015/02/26/sim-card-gemalto-says-it-was-hack-by-us-and-england-but-not-everyone-is-convienced/

另外，又有報導說網站傳輸最常用的SSL加密協定，很多網站因其選用的金鑰，實際長度只有512位元，而易受駭客攻擊。我認為這是美國人自己搞的，自作自受，這是因為如前述的，美國政府規定所有出口版本的軟硬體安全系統，所使用的金鑰長度都受限或者必須留所謂的基準金鑰給美國政府！（這樣好讓NSA可以輕易骇入外國網站或資訊系統！OK？斯諾登說的都是真的）
The weak 512-bit keys are a vestige of the 1990s, when the Clinton administration required weak keys to be used in any software or hardware that was exported out of the US. To satisfy the requirement, many manufacturers designed products that offered commercial-grade keys when used in the US and export-grade keys when used elsewhere. Many engineers abandoned the regimen once the export restrictions were dropped, but somehow the ciphers have managed to live on a select but significant number of end-user devices and servers.



“FREAK” flaw in Android and Apple devices cripples HTTPS crypto protection
Bug forces millions of sites to use easily breakable key once thought to be...
ARSTECHNICA.COM|由 DAN GOODIN 上傳

http://arstechnica.com/security/2015/03/freak-flaw-in-android-and-apple-devices-cripples-https-crypto-protection/　


）
  






 
張貼者： 於
標籤：